ニュースレターNo.44/2010年3月発行

暗号アルゴリズムの危殆化

今回のインターネット10分講座では、インターネットに関する技術に対して比較的影響が大きい、暗号アルゴリズムの危殆化について解説します。

1. はじめに

既にご存じの方も多いと思いますが、2010年1月7日に、複数の欧州の研究機関とNTTで構成される研究グループによって、768ビット（10進232桁）のRSAモジュラスである合成数の素因数分解に成功したという発表がありました（［1,2］）。RSAモジュラスとは二つの素数の積の形をした合成数です。素因数分解問題の困難性、言い換えますと、大きな桁数の合成数の素因数分解が難しいということが、多くの暗号プロトコル、および、暗号アルゴリズムの安全性を担保しているというのが、最も基本的な事項の一つです。

今回の記録達成は、現在多くのアプリケーションで使用されている、例えば1024ビットのRSAモジュラスなどの、より大きな桁数の合成数から見れば一つの通過点に過ぎませんが、素因数分解の困難性が有する安全性の評価のみならず、暗号アルゴリズムに関するパラメータ設定の移行時期、および、使用期限を予測する上で非常に重要な通過点です。

2. 暗号アルゴリズムの危殆化とは

簡単に言えば、暗号アルゴリズムの危殆化とは、暗号アルゴリズムの安全性のレベルが低下した状況、または、その影響により暗号アルゴリズムが組み込まれているシステムなどの安全性が脅かされる状況を言います。普通は、暗号アルゴリズムが破られたとか、解読されたとか言われますが、どの程度暗号アルゴリズムが破られたのか、解読されたのかが説明されないと詳しいことは分かりません。暗号アルゴリズムに対する解析方法は数多くあり、しかも、解析結果には非常に大きな幅があるので、専門家による解説がなければ一般の人には分かりません。

例えば、大雑把な分類として、

暗号アルゴリズムに問題点が見つかっていない。
暗号アルゴリズムの一部分に、ある欠陥が見つかっただけで、暗号アルゴリズムの全体の問題ではない
暗号アルゴリズムの全体にまで解析が及んでいるが、解読するためのコストが現実的な量ではない。
暗号アルゴリズムの全体にまで解析が及んでおり、解読するためのコストが現実的な量である

のような区別を付けることが考えられます。

また、コストについては、

時間的なコスト
金額的なコスト

の二つの量に分けられます。

本稿では例として、RSA暗号（素因数分解問題）、ハッシュ関数MD5とSHA-1の三つのケースを挙げて、もう少し詳細について見ていきます。

2.1 RSA暗号（素因数分解問題）の場合

素因数分解問題とは、二つの相異なる素数p,qの積である合成数Nが与えられた時に、Nだけからその素因数p,qを求める問題です。そして、RSA暗号は、1978年にリベスト（Rivest）、シャミア（Shamir）、エイドルマン（Adleman）の3人によって公表された公開鍵暗号の一つで、その安全性は素因数分解問題の困難性に依存しています。一般によく使われているRSA守秘やRSA署名もその一種です。公開されている公開鍵から秘密鍵が解かれてしまえば、暗号文の復号も、署名の偽造も可能になってしまいますから、RSAモジュラスの選択において、素因数分解問題の困難性は非常に重要な位置を占めています。

1990年頃になって、ポラード（Pollard）らの数学者によって一般数体ふるい法（General Number Field Sieve, GNFS）が提案されてからは、徐々に分解される合成数のサイズが大きくなってきました。一般数体ふるい法は、非自明な関係式

x² ≡ y²（ mod N）

を見つけて、最大公約数GCD（x±y,N）を計算することにより、Nの素因数を見つけ出すアルゴリズムで、

多項式選択
関係式収集
フィルタリング
線形代数計算
平方根計算

の五つのステップからなり、2.関係式収集、および、4.線形代数計算の二つのステップが計算量の大半を占めます。現在知られている解法アルゴリズムの中では最速ですが、最適化のためのパラメータ設定が複雑なのが特徴です。表1が分解記録リストです。

表1：一般数体ふるい法による近年の分解記録
合成数	サイズ	公表年月
RSA-768	232桁(768ビット)	2010年1月
RSA-200	200桁(663ビット)	2005年9月
RSA-640	193桁(640ビット)	2005年11月
11²⁸¹+1の約数	176桁(582ビット)	2005年4月
RSA-576	174桁(576ビット)	2003年12月
21⁸²⁶+1の約数	164桁(545ビット)	2003年12月
RSA-160	160桁(530ビット)	2004年4月
2⁹⁵³+1	158桁(524ビット)	2002年1月
RSA-155	155桁(512ビット)	1999年8月
RSA-140	140桁(463ビット)	1999年2月
RSA-130	130桁(430ビット)	1996年3月

実は、一般数体ふるい法の計算量は、以下のような漸近的な評価が与えられているのでおおよその推定は可能ですが、正確な計算量の予測にはあまり適していません。

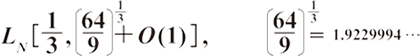
ただし、

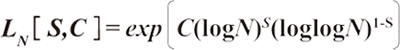
そこで、関係式収集ステップの計算量を部分的な実験結果から推定する方法を用いて、CRYPTREC^※1では素因数分解問題に関する評価結果を2006年度に公表しています^※2。

グラフ:処理性能予測 — 図1：1年間で関係式収集ステップを完了するのに要求されるコンピュータの処理性能予測（［3］からの引用）

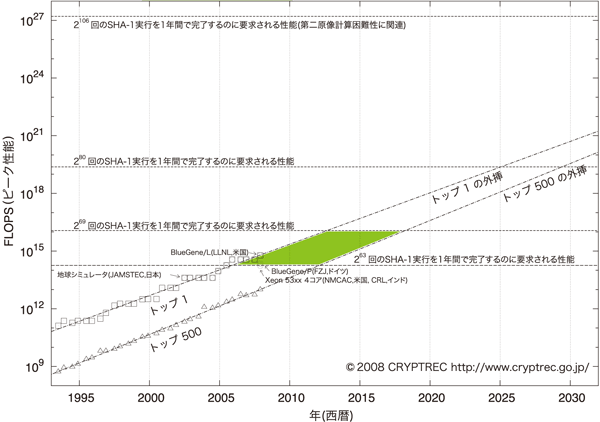
この評価結果から、分解にかけるコストに依存するものの、1024ビットのRSAモジュラスの素因数分解はおおよそ2015年.2020年頃から分解の可能性が高まってくるということが読み取れます。従って、今後、新規にシステムを構築する場合には、1024ビットよりも長いサイズのRSAモジュラスを選択することが望ましいものと考えられます。

移行に際してまずはじめに問題となるのは、次にどのビットサイズを用いるのかということです。PC環境においては2048ビットへ変更するのは比較的容易であっても、ICカードや携帯電話など記憶容量や計算能力といったリソースに制限がある場合には難しいことが考えられます。また、1024ビットの使用をいつまで認めるべきかという、使用期限の観点についても問題となってきます。

2.2 ハッシュ関数MD5の場合

MD5はリベストによって1991年に提案された、ブロック長が512ビット、ハッシュ長が128ビットであるハッシュ関数です。提案されてから数年後には、MD5の一部分に問題点が指摘され、MD5の仕様に変更を加えたハッシュ関数に対して、衝突を探索する攻撃アルゴリズムが発見されました。しかしその時はオリジナルのMD5の衝突発見までには至っていませんでした。

説明が前後しますが、一般にハッシュ関数Hの安全性には大きく分けて、以下の三つがあります。

衝突発見困難性－ハッシュ値が一致する、すなわち、H（M₁）=H（M₂）となるようなメッセージM₁とM₂を探索することが困難なこと。
第2原像計算困難性－ある既知のメッセージMとそれに対するハッシュ値が与えられた時に、ハッシュ値が一致する、すなわち、H（M）=H（M'）となるような別のメッセージM'を探索することが困難なこと。
原像計算困難性－ある未知のメッセージMに対するハッシュ値が与えられた時に、ハッシュ値が一致する、すなわち、H（M）=H（M'）となるようなメッセージM'を探索することが困難なこと。

ようやく、2004年になってワン（Wang）らによってMD5の衝突を効率的に探索するアルゴリズムが提案されました。ワンらは入力ブロックの一つ目と二つ目に差分を加え、それぞれのブロック、および、関数内部の内部変数に制約条件を与えることで、衝突探索の効率を著しく高めることに成功しています。

探索で計算されるメッセージのペアはランダムなデータなので、それ自体では意味をなすような文書になる確率は低いものです。つまり、普通のテキストファイルのような文書の範囲で、衝突を起こすようなメッセージのペアを見つけることは困難です。しかしながら、バイナリなメッセージを文書中に埋め込んでも文書フォーマットとして正当であるような場合には、衝突を起こすような文書を作成することが原理的には可能となります。

その顕著な例が、公開鍵暗号基盤（Public Key Infrastructure, PKI）の公開鍵証明書のメッセージフォーマットとして利用されているX.509証明書です。レンストラ（Lenstra）らはワンらがMD5の衝突探索アルゴリズムを提案してすぐさま2005年に、X.509証明書の衝突探索手法を提案しています。つまり、はじめは探索で計算された衝突メッセージを「modulus」フィールドに埋め込むことで衝突を起こすX.509証明書のペアを計算する手法でした。

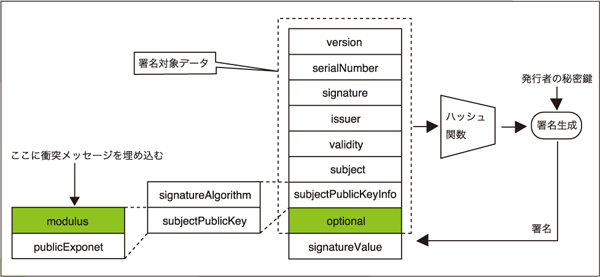
図:2005年時点のX.509証明書の衝突手法のあらまし — 図2：2005年時点のX.509証明書の衝突手法のあらまし

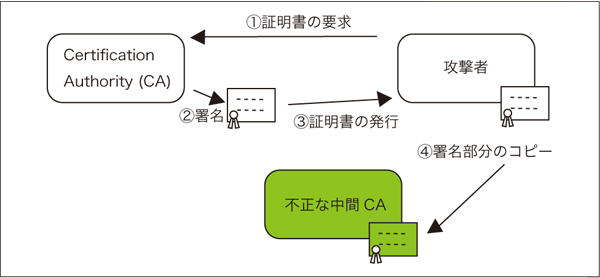
ところが、その後探索手法の研究の進展によって、レンストラらの研究チームは偽造したX.509証明書を商用のCA（Certification Authority）に実際に署名させることにより、中間CA証明書の偽造に成功するまでに至っています（［4］）。ここで重要なことは、前述の1.～3.とは異なる、新たな、

Chosen-Prefix衝突発見困難性－既知のメッセージP₁とP₂が与えられたときに、ハッシュ値が一致する、すなわち、H（P₁ ｜｜ S₁） = H（P₂ ｜｜S₂）となるようなメッセージS₁とS₂を計算することが困難なこと。

という探索アルゴリズムが提案されていることです。第2原像計算困難性を有していたとしても、この探索アルゴリズムのおかげで、より現実の状況に沿ったX.509証明書の偽造が可能になっています。また、探索で計算された衝突メッセージを埋め込む場所は図2における「optional」フィールドで、署名検証側にとって無意味な場合には読み飛ばす場所を利用しています。

この発表を受けて、ベリサイン社が2009年初めにMD5の証明書発行の停止を発表するなど、証明書発行ベンダー側での対応も早速なされています（［5］）。

図:2008年時点のX.509証明書偽造の様子 — 図3：2008年時点のX.509証明書偽造の様子

2.3 ハッシュ関数SHA-1の場合

SHA-1は米国の国立標準技術研究所（National Instituteof Standards and Technology, NIST）によって1995年に制定されたブロック長が512ビット、ハッシュ長が160ビットのハッシュ関数です。提案されてから10年近くの間、深刻な問題点が発見されていませんでしたが、MD5の衝突と同じ、ワンらによって2005年に衝突探索アルゴリズムが提案されています。

ワンらが提案した2005年頃の評価では、衝突探索に関する計算量は2⁶³～2⁶⁹の範囲でしたが、最近になってSHA-1の衝突探索アルゴリズムの計算量がさらに2⁵²まで低下しているとの報告がなされています（［6］）。

論文などにおいて公表されている、SHA-1の衝突探索に関する計算量をまとめると表2のようになります。

表2：MD5とSHA-1の衝突探索計算量低下の時間的流れ（[4]からの引用）
Year	MD5		SHA-1
Year	identical-prefix	chosen-prefix	identical-prefix	chosen-prefix
pe-2004	2⁶⁴	2⁶⁴		2⁸⁰
2004	2⁴⁰
2005	2³⁷		2⁶⁹ 2⁶³
2006	2³²	2⁴⁹		2^80-g
2007	2²⁵		2⁶¹
2008	2²¹
2009	2¹⁶	2³⁹	2⁵²

使用しているデータが古く、最新のデータをプロットしていませんが、CRYPTRECではSHA-1に関する評価結果を公表しています。

図:1年間で衝突を探索するのに要求されるコンピュータの処理性能予測 — 図4：1年間で衝突を探索するのに要求されるコンピュータの処理性能予測（［7］からの引用）

計算量が2⁵²まで低下しますと、SHA-1の衝突メッセージがいつ世界で初めて算出されても、現在のコンピュータの性能からいっておかしくはありませんが、本原稿の執筆時点においてはまだ発見されていません。なお、SHA-1については、MD5においてサーバ証明書を偽造することが容易になるほど、衝突探索アルゴリズムの効率は向上していませんが、そうでなくてもコンピュータの性能向上により安全性は徐々に低下していきますから、今後の動向には細心の注意が必要です。

3. 危殆化に係る問題点

暗号アルゴリズムはそもそも単体で用いられるものではなく、ソフトウェア、または、ハードウェアとして実現され、システムなどに組み込まれて初めて使われるものです。もう少し詳しく見ると、暗号アルゴリズムはソフトウェア、または、ハードウェアとして実現され、暗号モジュールを構成し、暗号モジュールは暗号プロトコルなどに組み込まれます。最後に、システムは実現したい要件に従って、暗号プロトコルなどを選択して自身に組み込んでいます。

問題になるのは、システムで使用しているある暗号アルゴリズムに危殆化が生じたとして、暗号アルゴリズムを交換したり、あるいは、暗号アルゴリズムのパラメータの設定を変更したりすることがはたして可能なのかということです。

残念なことに、暗号アルゴリズムの変更を考慮に入れてシステム構築がなされていることが非常に少ないのが現状です。

4. 移行スケジュールの策定の必要性

暗号アルゴリズムの変更を考慮に入れていない情報システムが多い中で、暗号アルゴリズムの移行指針とそのロードマップについて検討することは非常に重要です。

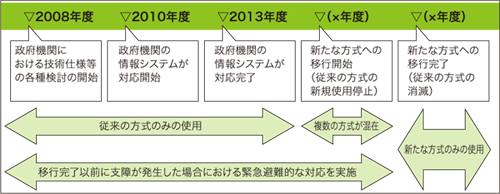
CRYPTRECにおいて2006年度に公表された、RSA1024ビットが有する素因数分解の困難性、および、SHA-1の衝突発見困難性に関する評価結果を受けて、政府機関の情報システムに関する情報セキュリティ対策を立案・遂行する機関である、内閣官房情報セキュリティセンター（National Information Security Center, NISC）は、政府機関の情報システムにおいて使用されているSHA-1、および、RSA1024ビットに係る移行指針を策定しています（［8］）。そこでは、政府認証基盤（Government Public Key Infrastructure, GPKI）などの電子政府システムにおいて、情報システムのライフサイクルに合わせて、SHA-256、および、RSA2048ビットが選択可能なように今後、システム設計をする旨、政府統一的な対応策が取られています。

図:移行スケジュール概念図 — 図5：移行指針に基づく暗号方式の移行スケジュール概念図

5. まとめ

本稿では、暗号アルゴリズムの危殆化の概要について駆け足で見てきました。海外の動向など他にもご紹介すべき点がたくさんあるのですが、紙面の都合で割愛せざるを得ませんでした。この場を借りてお詫びしたいと思います。最後に政府機関における移行指針について紹介しましたが、すべての民間企業においてコンセンサスが得られているわけではありません。重要なことは、それぞれの所属するコミュニティにおいて、主体的に暗号アルゴリズムの移行について検討することです。その中で、他のコミュニティとの調整が必要となってくる場合もあると思います。

（独立行政法人情報通信研究機構（NICT）/黒川貴司）

参考文献

[1]: Kleinjung,Aoki,Franke,Lenstra,Thome,Bos,Gaudry,Kruppa,Montgomery,Osvik,te Riele,Timofeev,Zimmermann“, Factorization of a 768-bit RSA modulus”
http://eprint.iacr.org/2010/006
[2]: NTTニュースリリース「公開鍵暗号の安全性の根拠である「素因数分解問題」で世界記録を更新～768ビット合成数を一般数体篩法にて完全分解に成功～」
http://www.ntt.co.jp/news/news10/1001/100108a.html
[3]: CRYPTREC「, CRYPTREC Report 2006」
http://www2.nict.go.jp/y/y213/cryptrec_publicity/c06_wat_final.pdf
[4]: Stevens,Sotirov,Appelbaum,Lenstra,Molnar,Osvik,Wegner,“ Short Chosen-Prefix Collisions for MD5 and the Creation of a Rogue CA Certificate”
http://eprint.iacr.org/2009/111
[5]: ベリサイン,「MD5アルゴリズムへの衝突攻撃によるSSLサーバ証明書の偽造に関する報道について」
https://www.verisign.co.jp/ssl/about/20090106.html
[6]: McDonald,Hawkes,Pieprzyk“,Differential Path for SHA-1 with complexity O（2⁵²）”
http://eprint.iacr.org/2009/259
[7]: 総務省・法務省・経済産業省,「電子署名及び認証業務に関する法律の施行状況に係る検討会」報告書
http://www.soumu.go.jp/menu_news/s-news/2008/080530_4.html
[8]: 内閣官房情報セキュリティセンター「,政府機関の情報システムにおいて使用されている暗号アルゴリズム SHA-1及びRSA1024に係る移行指針」
http://www.nisc.go.jp/active/general/res_niscrypt.html

※1: 電子政府推奨暗号の安全性を評価・監視し、暗号技術の適切な実装法・運用法を調査・検討するプロジェクト。総務省、経済産業省、独立行政法人情報通信研究機構、独立行政法人情報処理推進機構が事務局を運営している。
※2: 参考文献［2］によると、ふるい処理の計算量はAMD Opteron 2.2GHz換算で1500年と見積もられています。これは［3］の予測値の35%増であって、おおよそ予想の範囲内にあるものと考えられます。